tmp1

流星体燃尽机理

Dec 21st

@学而时习 | 564次浏览(views)

0条评论(comment)

流星体燃尽(ablation)机理

讲师：Oleg I. Belkovich

　　我们大家都知道，流星是流星体与大气摩擦发光产生的现象，绝大多数的流星体在这一过程中被燃尽，但有极少数的流星体没有燃尽就落到了地面，它们被称为陨石，于是每次流星雨时便会有半开玩笑的笑话：小心被流星砸中啊。然而，这似乎的确只是个笑话而已：到目前为止，历史上已知的陨石事件没有一个能被确认来自已知的流星雨。合理的解释是，根据脏雪球模型，绝大多数流星带都源自彗星核喷发出的物质：密度介于0.2-1g \cdot cm^{-3}的水冰-岩屑混合物；脏雪球模型在这些物质成为流星时同样适用。如果我们将一个随便捏成的雪团扔到火炉边，最可能出现的情况是它将不断分解成更多的小雪团，直到最终融化。同样，一个满足“脏雪球模型”的流星体在与大气分子撞击产生高温时，也将不断分解成更多的“小脏雪球”，直到最终燃尽。只有足够巨大的致密流星体才可能在不满足“解体后燃尽”的命运，落到地球上成为陨石。

　　为了能定量地观察流星体燃尽的过程，我们必须将打遍天下无敌手的武器——数学——拿出来。首先，我们从气象学上常用的压高公式开始：

p(h) = p(h_0)\exp(-\int_{h_0}^{h}\frac{dh}{H})

其中H = \frac{RT}{\mu g}是“特征高度”，R=8.314 J/mol \cdot K是波尔兹曼常数，T是温度，\mu = 29g/mol是空气分子质量，g是万有引力常数。压高公式的本质是气压与高度的关系。由于流星现象一般出现在80-120公里的高度上，可以近似地认为T是常数，因此上式化为

p(h) = p(h_0)\exp(-\frac{h-h_0}{H})

　　通过大气环流模型可以确定H大致在5.6-5.8km之间。

　　气压和流星有什么关系呢？关系可大了。气压本质上是竖直方向上空气分子浓度的积分，如果浓度太低，那流星体碰撞到的空气分子的数量不足，自然在亮度上就要打折了；这就是为什么理论计算认为火星上的流星雨普遍偏小而金星上的流星雨普遍偏大的缘故。各位有兴趣去金星上看流星雨吗？

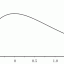
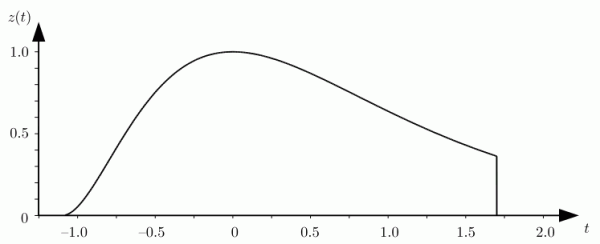
　　现在我们要介绍流星尾迹的离子化(ionization of the trail)。这是个极其重要的概念，尤其是在雷达流星技术上。即使是在日常观测中，大家也会对带着明亮尾迹的漂亮流星惊叹不已的。由于流星体的速度极高，和大气摩擦剧烈，因此在其路径上会产生自由电子。自由电子的产生率和流星体的截面及气压成正比。流星路径上每单位长度的自由电子数称为电子线密度，以\alpha表示。显然，根据观测经验，我们可以猜想出如下的电子线密度的变化：由0开始增加到极大值后缓慢回落，最后在某个大于0的值突然下降到0。或者这么说：电子线密度是个与高度有关的函数，即：\alpha (h) = \alpha _{max} \cdot z(h)。为了减少变量，我们将h标准化，引入相对高度t = \frac{h-h_{max}}{H}（其中h_{max}是\alpha _{max}对应的高度）。函数z(t)看起来如下面这个样子：

　　上图称为流星燃尽的“经典光变”，详情可参考Herlofson (1948, Repts. Prog. Phys. 11, 444)。不过，在实际观测中，电子线密度的值还和流星体的天顶距有关，显然天顶距越大，电子线密度越低。以\chi为天顶距，则可以看出\alpha _{max \chi} = \alpha _{max} \cos \chi，其中\alpha _{max \chi}代表观测者所见的实际电子线密度。

　　显然，根据上式，流星在某一时刻的电子线密度只取决于一个变量：\alpha _{max}。理论推出这个值的大小以目前技术水平来说几乎是不可能的，因此我们只能用观测方法给出它的定义：

\alpha _{max} = 4.03 \times 10^{14} \cdot \frac{m(v-8.15)^3}{H}

　　注意以上单位：流星质量m的单位是千克，速度v的单位是千米每秒，但特征高度H的单位是千米，而最终结果的单位是m^{-1}。

　　综合以上各式，可以得出电子线密度与高度的关系式：

\alpha _{max} = 4.03 \times 10^{14} \cdot \frac{m(v-8.15)^3}{H} \cdot \cos \chi \cdot z(\frac{h-h_{max}}{H})

单位仍然是m^{-1}。

　　以上我们将流星轨迹当作一条线段来看。但实际上，流星轨迹不能假设为一系列的点组成的，因为每个“点”实际上会随着时间的推移而变得弥散。这一弥散过程是满足一个不断变宽的高斯函数的。取以流星体中心为原点的极坐标，距离原点r处的自由电子密度与时间的关系式可以表示为：

n(r,t) = \frac{\alpha(h)}{\pi(r_0^2+4D_at)} \cdot \exp(-\frac{r^2}{r_0^2+4D_at})

其中有两个参数：初半径r_0和弥散系数D_a，分别代表零时刻的半径和弥散的速率。这仍然只能用经验公式来定义：

r_0 = 1.65 \cdot (\frac{v}{40})^(\frac{1}{2}) \cdot \exp (\frac{h-95}{2H})

D_a = 13.2 \cdot \exp (\frac{h-95}{H})

其中速度v的单位是千米每秒，特征高度H和高度h的单位是千米，r_0和D_a的单位分别是m和m^2 \cdot s^{-1}。

　　最后我们介绍“特征高度”的概念。从观测者的角度，对于某一流星群的成员，它们都具有几乎一致的密度、速度和天顶角。通过观察\alpha (h)式可以注意到，选取一个最小的\alpha _{max}，等价于选取一个最大的h。这是什么意思呢？简单来说，流星体是不能无止境地小下去的，肯定有一个极限（这个极限对应于质量为10^{-8}g的流星体），超过这个极限之后，流星体就不能产生观测者能观测到的流星现象了（注意，并不是说它不产生流星现象了，只是观测者没有能力观测到而已）。选取这个极限等价于选取\alpha _{max}的最小值，也等价于选取h。我们将这个h=h_0称为“特征高度”(characteristic height)。由于电子线密度与天顶角有关，对于观测者来说的特征高度显然也与天顶角有关，经验公式为：

h_{0,\chi} = h_{0,0}-0.35H \cdot \ln \cos \chi

其中h_{0,\chi}代表观测者所见的特征高度，h_{0,0}代表理想条件（辐射点在天顶）的特征高度。以上公式对于质量小于下限或致密流星体也成立。

　　由于流星群的成员之间具有相同的速度、密度和天顶角，显然，每一个流星群都有一个固定的特征高度。雷达作为最灵敏的观测手段，可以观测到在特征高度上达到“最亮”的流星（即：质量恰在下限的流星体）；稍大一点的流星体有足够的物质被燃烧，因此达到“最亮”的高度低于特征高度，故可以被略微不灵敏的探测手段（比如摄像或者目视）观测到。质量达不到下限的流星体无法进入燃尽过程，因此最终会以液态到达地面。有关特征高度的实际测定，可参考Evans (1954, MNRAS, 114, 63) Sect. 5。

, ,

流星带基础理论

Dec 20th

@学而时习 | 823次浏览(views)

2条评论(comments)

按：与电动力学火拼之后，终于可以腾出时间来阅读四个月来导师塞来的一叠论文了，其中有一份2005年比利时“雷达流星交流会”的学习材料，由若干篇短小的综述组成，共计130页，比较全面地介绍了流星、尤其是雷达流星方面的理论入门，有些内容还是蛮有意思的，于是我决定学习的同时也将笔记记在博客上，供有兴趣的朋友参考。

流星带(meteor stream)基础理论

讲师：Oleg I. Belkovich

　　每一流星雨都来自于某一特定的流星带（英文meteor swarm或meteor stream，国内似未有标准译法，有翻译为“流星群”的，但个人认为不妥，故译为“流星带”），这便是我们讨论的出发点。流星带系由其母体喷洒出的微粒组成的带状微粒流，在与母体相似的轨道上围绕太阳运转。若流星带与地球轨道相交，则地球在穿过流星带时，部分微粒会落入大气层中形成流星，由于其速度矢量几乎完全一致，在地面观测者看来便是反向延长线交于同一点（严格来说是一个比较小的区域）的流星雨现象。

　　即使是一般大众也知道流星有亮暗之分，不同流星雨的亮暗比例也有所不同。简单来说，亮流星对应大颗粒，暗流星对应小颗粒。大小颗粒在流星带中是不是随机分布的呢？非也。于是我们要涉及到第一个物理概念：坡印廷-罗伯逊效应(Poynting-Robertson effect)。

　　看到坡印廷的名字立即让我想到电磁学里的坡印廷矢量。不错，这个效应和坡印廷矢量（或者说是能流矢量）有关，但理解起来还是挺容易的。我们在雨中骑车的时候，理论上雨滴是会对我们造成阻力的（当然这个阻力比空气阻力小太多了，可以忽略不计，除非雨特别大）。在真空的宇宙中，自然不会有空气阻力，但来自太阳的电磁波这时造成了另一种阻力，使得在轨道上运动的物体的角动量略微减小。对于大的物体，比如行星、宇宙飞船等，这一效应可以忽略不计；但对于微粒来说，这一效应就比较明显了。因此可以显然做出一个定性的推断：对越小的微粒，这一效应就越明显。坡印廷-罗伯逊效应的强度可以用以下公式表示：

F_{\rm PR} = \frac{r^2 L_{\rm s}}{4 c^2}\sqrt{\frac{G M_{\rm s}}{R^5}}

其中F_{\rm PR}代表物体的受力，r代表颗粒物直径，L_{\rm s}代表太阳光度，M_{\rm s}代表太阳质量，R代表颗粒物的轨道半径，G和c分别代表万有引力常数和光速。可以看出，F_{\rm PR}与r^2成正比。对于上述公式的详细推导可以参阅 Guess (1962, ApJ, 135, 855) 。

　　由于万有引力是与r^3成正比，可以证明对于小的物体而言，F_{\rm PR}更为显著。同时F_{\rm PR}与R^{-2.5}成正比，与万有引力定律比较可以注意到，在R较小时F_{\rm PR}的效应会更显著。由于角动量守恒，这一效应将使得颗粒的轨道偏心率变小。因此，坡印廷-罗伯逊效应的结果是：流星云会变得越来越“弥散”，外围是较大的颗粒物，而内侧则是较小的颗粒物，地球可能可以在短时间内（比如几天之内）分别穿过较大和较小颗粒物占多数的部分。如果流星带具有一定的倾角，那倾角较高的是较大的颗粒物，倾角较底的是较小的颗粒物；对于这种情况，地球可能只能穿过流星带中，某一直径的颗粒较多的部分；因为其他直径颗粒在“上面”（或者下面）。

　　很好。现在我们知道颗粒物是有大有小的，而且它们并不是随机分布的；换句话说，当地球穿越某一流星带的时候，不同直径的颗粒物的数量比并不是一成不变的，更不要说不同流星带之间的差异了。总之，为了能构造一个流星带模型出来，我们首先需要的就是不同直径的颗粒物的数量比。回忆微积分里定义某个参量的办法，我们将定义质量比s定义如下：设微粒的质量分布函数为p(m)质量介于m和m+dm之间的微粒数与m^{-s}成正比。因此，直径大于m_{0}的颗粒的数量可以通过以下算式得出：

\frac{N(m_{0})}{N(m_{total})} = \frac{\int_{m_{0}}^{\infty} p(m) dm}{\int_{0}^{\infty} p(m) dm} = (\frac{m_{0}}{m_{total}})^{1-s}

　　由于微粒的数目显然和流星流量密度定义相同，因此

\frac{Q(m_{0})}{Q(m_{total})} = (\frac{m_{0}}{m_{total}})^{1-s}

其中Q(m)代表质量在(m,+\infty)之间的微粒的流量密度。通过取对数消去指数项，可以注意到\lg Q(m)和\lg m呈线性关系，其斜率为1-s。这对于以后的讨论很有益。

　　然而，实际观测中s用的并不多，较常用的是星等m（对于目视观测）或者电子线密度\alpha（对于雷达观测）。在目视观测中，r（注意这里的m,r不能和常用的质量、半径混淆）被定义为族群指数(population index)，意为每增加一个星等，流星增加的倍数。根据 Koschack & Rendtel (1990, WGN, 18, 118) 的结果，s,r之间的关系为

-(1-s) = 2.3 \lg r

其中系数2.3是普森公式的2.5乘上一个经验系数得来。

,